
트리 (Tree)
Tree란?
트리는 영어 단어 그대로 가지가 뻗어 있는 모양으로 노드와 간선으로 구성된 그래프의 일종이다. 그래프와 다른 점은 하나의 노드에서 다른 노드로 이동하는 경로가 유일하다는 점이다. 이를 Acycle이라고 한다. 트리는 폴더 구조, 조직도, 가계도 등 계층적 구조를 나타날 때 사용 한다.
트리의 구조
트리 구조의 자료 값을 담고 있는 단위를 노드(Node)라고 한다. 그리고 노드 간의 연결선을 에지(Edge)라고 한다. 이렇게 연결된 두 노드 중 상위의 노드를 부모(Parent) 노드, 하위의 노드를 자식(Child) 노드라고 한다. 그리고 같은 부모를 가지는 노드를 형제(Sibling) 노드라고 한다. 자신을 포함한 자식 노드의 개수를 크기(Size)라고 하며, 각 노드가 지닌 에지(가지)의 수를 차수(Degree)라고 한다. 이때 트리에서 최대 차수가 곧 트리의 차수이다.
트리 자료 구조는 가장 상위의 노드를 시작으로 왼쪽 자식 노드, 오른쪽 자식 노드로 뻗어 나가는 모양이다. 이때, 트리의 노드 중 가장 상위의 노드, 즉 부모가 없는 노드를 루트(Root) 노드라고 한다. 그리고 자식이 없는 노드를 잎새(Leaf) 노드 혹은 단말 노드라고 한다.
루트 노드에서 어떤 특정 노드까지의 간선의 수를 깊이(Depth), 이러한 특정 깊이를 가지는 노드의 집합을 레벨(Level)이라고 한다. 트리에서 가장 큰 레벨 값을 높이(Height)라고 한다.

트리의 특징
- 트리는 하나의 노드에서 다른 노드로 이동하는 경로가 유일하다. 이를 사이클이 존재하지 않는다(Acycle)라고 하며 사이클이 존재할 경우 트리가 아니라 그래프이다.
- 노드가 N개인 트리의 Edgd의 수는 N-1개이다.
- 모든 노드는 서로 연결되어 있다.
- 하나의 Edge를 끊으면 2개의 서브트리(Sub-Tree)로 분리된다.
이진트리(Binary Tree)
각 노드가 최대 2개의 자식노드를 가지는 트리를 이진트리라고 한다. 이때 자식 노드는 좌우를 구분한다.
포화 이진 트리(Perfect Binary Tree)
모든 레벨에서 노드들이 꽉 채워져 있는 트리를 포화 이진트리라고 한다.

완전 이진 트리(Complete Binary Tree)
마지막 레벨을 제외하고 노드들이 모두 채워져 있는 트리를 완전 이진트리라고 한다.
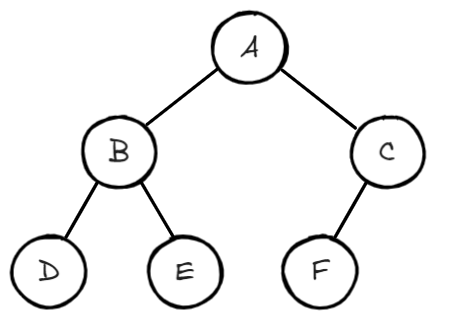
정 이진 트리(Full Binary Tree)
모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리를 정 이진트리라고 한다.
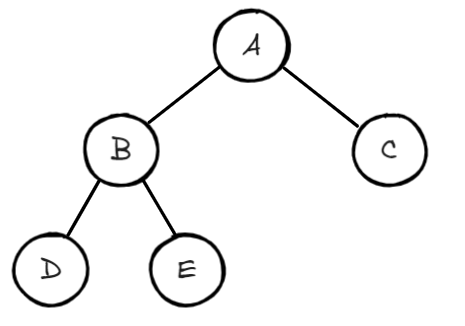
편향 트리(Skewed Binary Tree)
한쪽으로 기울어진 트리를 편향 트리(사향 트리)라고 한다.

균형 이진 트리(Balanced Binary Tree)
모든 노드의 좌우 서브 트리 높이가 1 이상 차이 나지 않는 트리를 균형 이진트리라고 한다.


이진트리의 특징

- 포화 이진 트리의 높이가 ((h))일 때, 노드의 수는 ((2^{h+1} - 1))개 이다.
- 포화(or 완전) 이진트리의 노드가 ((N))개 일 때, 높이는 ((logN))이다.
- 이진트리의 노드가 ((N))개 일 때, 최대 가능 높이는 ((N))이다.
이진 트리의 순회 (Traversal)
모든 노드를 중복하지 않고 방문하는 연산하는 방법은 4가지가 있다.
이 중 전위, 중위, 후위 순회 방법은 DFS(Depth First Search)와 관련된 순회이고, 레벨 순회는 BFS(Breadth First Search)와 관련된 순회 방법이다.
순회 시 주의 점은 트리를 부모 노드 - 왼쪽 자식 노드 - 오른쪽 자식 노드 세 노드를 가지는 부분 트리로 생각하고 순회하되 자식 노드가 순회될 때 그 자식 노드도 다른 부분 트리의 부모 노드가 된다는 점을 생각하며 순회해야 한다. 즉, 전위 순회에서 루트 노드를 시작으로 왼쪽 자식 노드를 순회할 때, 그 왼쪽 자식 노드가 다른 자식 노드를 가진다면 그 자식 노드들을 본인의 형제 노드인 루트 노드의 오른쪽 자식보다 먼저 순회해야 한다는 점이다. 이점만 유의하면 전위, 중위, 후위 순회의 경우 루트 노드의 순회 순서가 가장 앞인지 중간인지 뒤인지만 바꿔주면 되므로 어렵지 않을 것이다.
전위 순회 (Preorder Traversal)
루트 노드를 가장 먼저 순회하는 방법이다.
방문 순서 : 루트 노드 -> 왼쪽 노드 -> 오른쪽 노드

중위 순회 (Inorder Traversal)
왼쪽 자식 노드를 순회한 후 루트 노드를 순회하는 방법이다.
방문 순서 : 왼쪽 노드 -> 루트 노드 -> 오른쪽 노드

후위 순회 (Postorder Traversal)
루트 노드를 가장 마지막에 순회하는 방법이다.
방문 순서 : 왼쪽 노드 -> 오른쪽 노드 -> 루트 노드

레벨 순회 (Levelorder Traversal)
위쪽 레벨의 노드의 왼쪽 노드부터 오른쪽 노드로 진행해 가며 순회하는 방법이다.

이진트리 구현
자바에서는 배열이나 연결리스트를 이용해 이진트리를 구현할 수 있다.
배열로 이진트리를 구현하였을 경우 인덱스를 통해 빠르게 노드에 접근할 수 있기 때문에, 특정 노드를 찾거나 접근할 때 효율적이다. 하지만 동적으로 크기가 변할 경우 새로운 배열을 생성하고 모든 요소를 복사해야 하는 단점이 있다.
연결리스트로 이진트리를 구현하였을 경우 동적으로 크기가 변하는 경우에도 유연하게 대응할 수 있고, 실제로 사용되는 노드에만 메모리가 할당되므로 배열 방식에 비해 메모리를 효율적으로 사용할 수 있지만, 특정 노드에 접근하기 위해서는 Head부터 연결을 따라가야 하기 때문에, 접근 시간이 더 걸릴 수 있다. 또한 실제 데이터만 저장하는 배열에 비해 자식 노드를 가리키는 포인터(참조)를 저장해야 하므로, 실제 데이터 외에 추가적인 메모리가 필요하다.
구현에 있어서는 배열 방식은 비교적 간단하므로, 연결리스트를 이용해 구현해 보고자 한다.
기본 구조는 다음과 같다. 노드에 해당하는 Node 클래스는 실제 데이터와 왼쪽, 오른쪽 자식 노드에 대한 참조를 멤버 변수로 가진다.
그리고 기본 생성자를 작성해 주었다.
class Node {
char data;
Node left;
Node right;
public Node(char data, Node left, Node right) {
this.data = data;
this.left = left;
this.right = right;
}
}이진트리 구조에 해당하는 BinaryTree 클래스는 루트 노드인 head를 가진다. 인스턴스 생성 시 char 배열을 입력받고 Node 객체의 배열인 nodes에 데이터 값과, 좌우 자식노드 값 (우선은 null)을 가지는 Node 객체를 새롭게 생성해 주소를 할당해 준다. 그리고 nodes를 다시 한번 순회하며 좌우 자식 노드를 가리킬 수 있도록 해주어 노드들을 연결한다. 최종적으로 head가 루트노드를 가리킬 수 있도록 해주면 head부터 따라가며 모든 노드를 탐색할 수 있게 된다.
class BinaryTree {
Node head;
public BinaryTree(char[] arr) {
Node[] nodes = new Node[arr.length];
for (int i = 0; i < arr.length; i++) {
nodes[i] = new Node(arr[i], null, null);
}
for (int i = 0; i < arr.length; i++) {
int left = i * 2 + 1;
int right = i * 2 + 2;
if (left < arr.length) {
nodes[i].left = nodes[left];
}
if (right < arr.length) {
nodes[i].right = nodes[right];
}
}
this.head = nodes[0];
}
}이제 이진트리의 순회를 구현해보자.
먼저 전위, 중위, 후위 순회의 경우 현재 노드(부모 노드)의 출력 순서만 다를뿐 구현 방법은 동일하다. 재귀 형태로 왼쪽 자식 노드, 자식 노드를 호출 하되 각각의 순회 방식에 맞게 현재 노드를 출력해주면 된다.
public void preOrder(Node node) {
if (node == null) {
return;
}
System.out.print(node.data + " ");
this.preOrder(node.left);
this.preOrder(node.right);
}public void inOrder(Node node) {
if (node == null) {
return;
}
this.inOrder(node.left);
System.out.print(node.data + " ");
this.inOrder(node.right);
}public void postOrder(Node node) {
if (node == null) {
return;
}
this.postOrder(node.left);
this.postOrder(node.right);
System.out.print(node.data + " ");
}레벨 순회의 경우 큐 자료구조를 활용한다. 큐에 탐색의 첫 시작이 되는 노드를 우선 넣어주고, 반복문을 돌며 큐의 첫번째 요소를 꺼내 출력해 주고, 좌우 자식노드가 존재 할 경우 이를 다시 큐에 넣어준다. 이렇게 레벨 순회의 탐색 순서에 맞게 레벨 별로 순서대로 탐색해가면서 큐에는 그 다음 탐색 할 자식 노드가 쌓이게 된다.
public void levelOrder(Node node) {
Queue<Node> queue = new LinkedList<>();
queue.add(node);
while (!queue.isEmpty()) {
Node cur = queue.poll();
System.out.print(cur.data + " ");
if (cur.left != null) {
queue.add(cur.left);
}
if (cur.right != null) {
queue.add(cur.right);
}
}
}
전체 코드
import java.util.LinkedList;
import java.util.Queue;
class Node {
char data;
Node left;
Node right;
public Node(char data, Node left, Node right) {
this.data = data;
this.left = left;
this.right = right;
}
}
class BinaryTree {
Node head;
public BinaryTree(char[] arr) {
Node[] nodes = new Node[arr.length];
for (int i = 0; i < arr.length; i++) {
nodes[i] = new Node(arr[i], null, null);
}
for (int i = 0; i < arr.length; i++) {
int left = i * 2 + 1;
int right = i * 2 + 2;
if (left < arr.length) {
nodes[i].left = nodes[left];
}
if (right < arr.length) {
nodes[i].right = nodes[right];
}
}
this.head = nodes[0];
}
public void preOrder(Node node) {
if (node == null) {
return;
}
System.out.print(node.data + " ");
this.preOrder(node.left);
this.preOrder(node.right);
}
public void inOrder(Node node) {
if (node == null) {
return;
}
this.inOrder(node.left);
System.out.print(node.data + " ");
this.inOrder(node.right);
}
public void postOrder(Node node) {
if (node == null) {
return;
}
this.postOrder(node.left);
this.postOrder(node.right);
System.out.print(node.data + " ");
}
public void levelOrder(Node node) {
Queue<Node> queue = new LinkedList<>();
queue.add(node);
while (!queue.isEmpty()) {
Node cur = queue.poll();
System.out.print(cur.data + " ");
if (cur.left != null) {
queue.add(cur.left);
}
if (cur.right != null) {
queue.add(cur.right);
}
}
}
}
public class treePractice {
public static void main(String[] args) {
// Test code
char[] arr = new char[10];
for (int i = 0; i < arr.length; i++) {
arr[i] = (char) ('A' + i);
}
BinaryTree bt = new BinaryTree(arr);
System.out.println("== Preorder ==");
bt.preOrder(bt.head);
System.out.println();
System.out.println("== Inorder ==");
bt.inOrder(bt.head);
System.out.println();
System.out.println("== Postorder ==");
bt.postOrder(bt.head);
System.out.println();
System.out.println("== Levelorder ==");
bt.levelOrder(bt.head);
System.out.println();
}
}
메인 메서드를 실행시켜 보면 각 순회 방식에 맞게 출력이 되고 있음을 알 수 있다. 이렇게 비선형 자료구조 트리의 특징을 알아보았고 자바를 이용해 구현까지 해보았다.
'자료구조 > 비선형 자료구조' 카테고리의 다른 글
| [Java]힙(Heap) 자료구조 (0) | 2023.12.17 |
|---|

